Roberto Serrentino
Introducidos algunos conceptos sobre el uso de fractales en Arquitectura, es importante precisar qué tipos de fractales existen, clasificarlos de acuerdo con sus atributos y características, y determinar cuáles de ellos son más adecuados para su utilización en esta disciplina. Sin embargo es conveniente primero recurrir a una clasificación convencional para la representación de todas las variantes de fractales. Para abordar la clasificación de lo general a lo particular, podemos dividirlos en dos grandes grupos: los fractales determinísticos (que a su vez pueden ser algebraicos o geométricos), y los fractales no determinísticos (también denominados estocásticos). Esta clasificación hace referencia al procedimiento seguido para su generación. En los determinísticos el proceso generativo queda pautado de antemano mediante una fórmula algebraica o algoritmo geométrico de reemplazo e iteración. En los no determinísticos, los procesos generativos están afectados por parámetros accidentales o aleatorios que permiten emular objetos fractales de apariencia más natural.
Los determinísticos algebraicos, creados mediante procesos algebraicos no lineales en espacios n- dimensionales, conforman la mayor clase de fractales. Los más estudiados son los que responden a procesos generativos bidimensionales, interpretando el proceso iterativo no lineal como un sistema dinámico discreto, por lo tanto es común referirse a estos fractales con terminología de la Teoría de Sistemas Dinámicos. Estos sistemas dinámicos no lineales transitan por diversos estados, y la manera en que el sistema se encuentra al cabo de varias iteraciones, depende de su estado inicial y de la descripción algebraica del proceso mediante una fórmula matemática, generalmente sencilla. Cada uno de estos estados, considerado como el resultado parcial de un proceso iterativo entre otros dos estados, expone una situación particular denominada atractor, que proviene de una porción de área del estado anterior y, al continuar iterando, termina en otra situación de atractor, correspondiente a un estado posterior, y así siguiendo hasta alcanzar un estado final al detener las iteraciones. De este modo, las distintas fases de espacialidad en el sistema se divide en áreas de atracción. Si en un espacio bidimensional se “pintan” con distintos colores las fases correspondientes a las mencionadas áreas de atracción, se obtiene un “retrato coloreado del área de atracción” en esa fase del sistema correspondiente a ese momento del proceso iterativo. Al cambiar el algoritmo de selección de colores se obtienen complicadas imágenes fractales con fantásticos trazos multicolores.

Tres áreas de atracción del mismo proceso iterativo
Los fractales determinísticos geométricos, son los que siguiendo una o más reglas de transformación de una figura derivada de la geometría estándar, permite obtener copias de ella misma, reducidas de tamaño (conceptos de autosemejanza y de independencia de escala).

Ejemplo de iniciador y generador pentagonal en 5 iteraciones
En el caso bidimensional se construyen a partir de una línea que se rompe y se transforma, o en el caso tridimensional a partir de una superficie 3D o de un volumen. El elemento que se toma como base es el iniciador y la regla de transformación geométrica es el generador. En el ejemplo de la Figura 2, el iniciador es un pentágono regular, y el generador es una regla que hace rotar 180 grados al pentágono original, reduce su área en un factor tal que a cada una de sus aristas se le adosen pentágonos perfectamente regulares, y el conjunto de seis pentágonos resultante se encuentre inscripto en el pentágono de la fase anterior. Se muestran cinco iteraciones de este proceso.

Iniciador y generador que incluyen curvas, y las dos primeras iteraciones
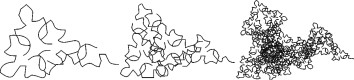
Cuarta, quinta y sexta iteración, aplicando el mismo generador.
También es posible describir este algoritmo simplemente como el reemplazo de cada arista del polígono original por una línea quebrada en cuatro segmentos, de tal manera que cumpla con el requerimiento que sus puntos más internos formen los vértices de un pentágono invertido. Cada uno de los segmentos que forma la línea quebrada es reemplazado por una nueva línea quebrada en la escala correspondiente a ese paso del algoritmo. Como resultado de la infinita repetición de estos pasos se obtiene un fractal geométrico. Con el mismo criterio puede proponerse algoritmos de reemplazo que operen con líneas curvas, o con una combinación de curvas y rectas, como se ve en el ejemplo de la siguiente figura.

Procedimiento generativo de paisajes fractales
Los fractales no determinísticos, denominados estocásticos, son aquellos en los que el procedimiento generativo conlleva la introducción de parámetros aleatorios, de la misma manera que los objetos naturales están afectados por numerosos factores externos que implican modificaciones inesperadas en su crecimiento o conformación. Ejemplos de fractales estocásticos bidimensionales son los que provienen de algoritmos en los que se introduce aleatoriedad, como en el caso de representación de la superficie del mar, o de topografía de un terreno de gran dimensión, casos en que predomina la tendencia al plano horizontal pero sin embargo están afectados por picos de tridimensionalidad.
Los denominados “paisajes fractales” se obtienen a partir de la técnica de subdivisión espacial que da como resultado superficies que se asemejan a terrenos naturales. Veamos un ejemplo donde se arranca con una figura geométrica, en este caso un cuadrado sobre el plano XY, que se subdivide en 4 partes iguales. Luego se provoca una perturbación vertical sobre cada uno de los 5 nuevos vértices, modificando su posición en la dirección del eje Z en una cantidad aleatoria. A continuación se repite el procedimiento con cada nuevo cuadrado, cada vez más pequeño, haciendo que las perturbaciones vayan decreciendo en cada iteración.
No parece difícil generar estos paisajes fractales mediante un algoritmo programado, sin embargo hay que disponer de varios “filtros” o “controles” que regulen su formación. He aquí una pequeña lista de los parámetros de control habitualmente disponible en esta clase de software:
- Una “semilla” generadora del número aleatorio inicial; esto significa que es posible reproducir el mismo paisaje fractal recordando un solo número que inicializa la secuencia de modificaciones en el algoritmo
- Un parámetro de rugosidad, que se aplica como factor de reducción de perturbaciones en cada iteración. Supongamos que el valor por defecto sea igual a 2. Valores menores que 2 dan como resultado terrenos con mayor rugosidad, y valores mayores que 2 dan como resultado terrenos más suaves.
- Un valor de perturbación inicial, que sirve para establecer la altura máxima del terreno; a partir de allí las perturbaciones van en orden decreciente unos puntos iniciales, que normalmente se los fija en las esquinas del rectángulo inicial. De esta manera se tiene un cierto grado de control sobre la apariencia global del terreno
- Un nivel de cota cero, también llamado nivel del mar, que simula el nivel natural del agua para marcar una diferencia entre lo que está por encima de esta cota (prominencias), y lo que está por debajo (depresiones).
- Un rango de colores, que se utiliza para iluminar y sombrear la superficie del terreno, tomando como base sus diferentes alturas. Normalmente se definen dos o tres colores en correspondencia con dos o tres alturas y luego se interpola linealmente entre estos puntos
-
Un número de iteraciones, que se establece en función de la densidad requerida para la malla que representa la superficie del terreno.
Estos fractales están basados en procesos que pueden ser usados para representar la geometría de diferentes entornos naturales (árboles, nubes, montañas). A través del mismo método recursivo, las ramificaciones de los árboles se abren y crecen con un rango de irregularidad aparente que pueden ser comparables a los más sofisticados ejemplos de geometría fractal. Pero debemos realizar una distinción entre esta aproximación y la forma real. Cada forma del árbol es única basada en numerosas tensiones naturales: luz solar, viento, exposición al clima y a otras condicionantes de su ambiente. La teoría de las formas de Platón reconoce este problema sugiriendo que cada árbol es una sombra o una aproximación de lo ideal, que es lo real. En esta visión cosmológica todos los intentos de representación de lo ideal resultan ser una copia imperfecta. Uno de los aspectos más sobresalientes del entorno natural es su variedad infinita. Cada árbol es una forma única, pero también existen muchos elementos comunes entre los miembros de una misma especie. Los fractales más constreñidos, más densos y complejos, son aquellos que exhiben autosemejanza en lugar de autoexactitud a través de todas las escalas. Las construcciones algorítmicas como el caso del terreno mostrado como ejemplo de geometría fractal, no exhiben la vivacidad que puede ser encontrada en el conjunto de Mandelbrot, de Julia, de Lyapunov, o de tantos otros ejemplos de fractales no lineales. Ellos son visualmente complejos, pero no ofrecen la variedad de formas naturales.
A lo largo de la historia, muchos matemáticos y estudiosos del tema fractales han propuesto sistemas generativos o procedimientos de representación, que han ampliado el rango clasificatorio de los mismos. Así que en muchos casos es posible obtener la misma representación de un fractal siguiendo procedimientos diferentes. O bien un fractal que deriva de la geometría estándar puede ser construido “a mano” (con métodos de dibujo tradicionales), o utilizando un sistema de funciones iterativas por computadoras, o un algoritmo de Lindenmayer también llamado Sistemas-L, etc. Cualquiera sea el sistema utilizado, habrá siempre áreas de atracción de formas que por iteración se concentran en zonas muchas veces inesperadas, dando lugar a la presencia de un atractor. Si este atractor conlleva un comportamiento dinámico en movimiento caótico, donde ni el lugar de su recorrido ni el tiempo en que lo recorre nunca son idénticos, en ese caso estamos en presencia de un atractor extraño, otra clase de fractal de la que hablaremos más adelante.
El texto pertenece al libro Contribuciones a los sistemas de diseño, 20 años del Laboratorio de Sistemas de Diseño, Editor: Leonardo Combes, Ediciones Magna, Tucumán, 2003.
-
La primera parte de este artículo fue publicada aquí
-
La segunda parte de este artículo fue publicada aquí
-
La tercera parte de este artículo fue publicada aquí

Pingback: Clasificación en tipos fractales [2da parte] | Fractales y arquitectura
Pingback: Arquitectura: ¿desde la forma al propósito o desde el propósito a la forma? (1ra parte) | Fractales y arquitectura
Pingback: Arquitectura: ¿desde la forma al propósito o desde el propósito a la forma? (2da parte) | Fractales y arquitectura
Pingback: Conclusiones | Fractales y arquitectura